


《圆周角》圆PPT
第一部分内容:圆周角
你还记得圆心角的定义吗?
顶点在圆心的角,叫做圆心角.
顶点在圆上,并且两边都和圆相交的角,叫做圆周角.
探究
分别测量图中弧AB所对的圆周角∠ACB和圆心角∠AOB,它们之间有什么关系?
改变C点的位置,再次测量∠ACB 和∠AOB,这个关系还成立吗?
改变B点的位置,再次测量∠ACB 和∠AOB,这个关系还成立吗?
分析
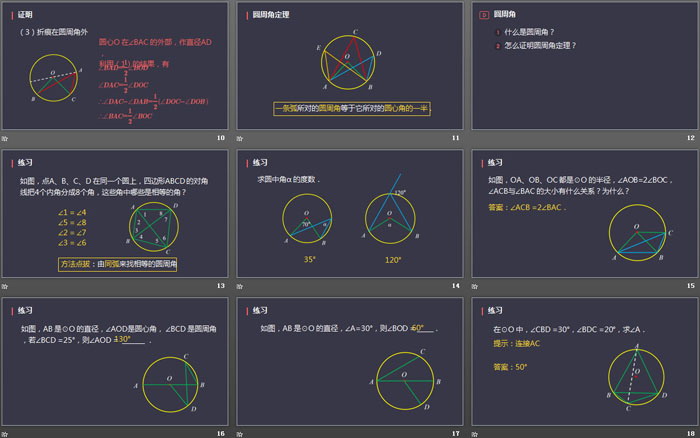
为了进一步探究上面的发现,如图在⊙O 任取一个圆周角∠BAC,将圆对折,使折痕经过圆心O 和∠BAC 的顶点A.由于点A的位置的取法可能不同,这时折痕可能会出现三种情况:在圆周角的一边上 在圆周角内 在圆周角外
... ... ...
圆周角PPT,第二部分内容:圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
练习
如图,点A、B、C、D 在同一个圆上,四边形ABCD 的对角线把4个内角分成8个角,这些角中哪些是相等的角?
方法点拔:由同弧来找相等的圆周角
如图,OA、OB、OC 都是⊙O 的半径,∠AOB=2∠BOC,∠ACB与∠BAC 的大小有什么关系?为什么?
答案:∠ACB =2∠BAC.
思考题
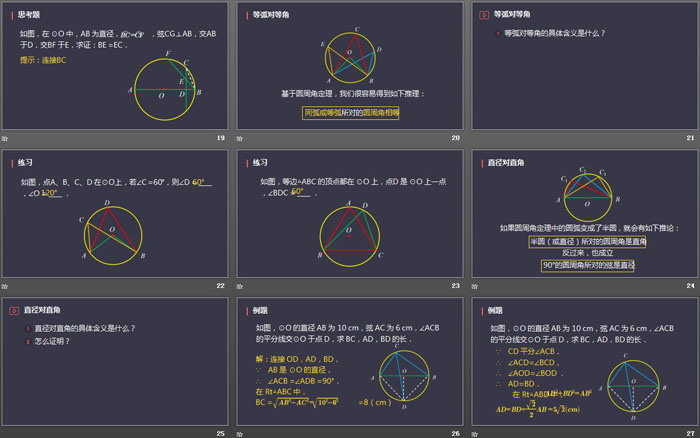
如图,在 ⊙O 中,AB 为直径,BC=CF,弦CG⊥AB,交AB 于D,交BF 于E.求证:BE =EC.
提示:连接BC
... ... ...
圆周角PPT,第三部分内容:等弧对等角
基于圆周角定理,我们很容易得到如下推理:
同弧或等弧所对的圆周角相等
练习
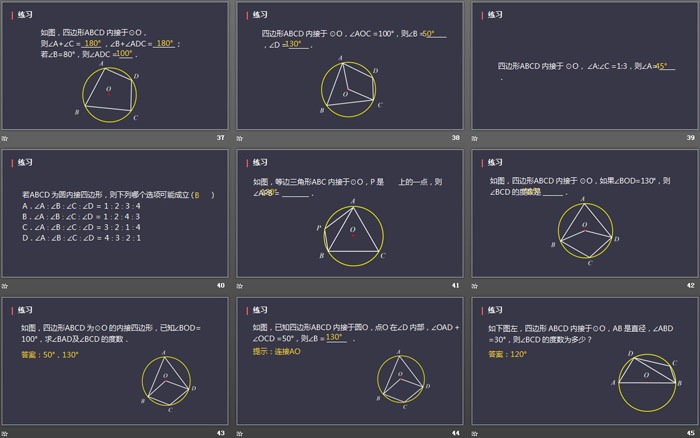
如图,点A、B、C、D 在⊙O上,若∠C =60°,则∠D = ____ ,∠O = ____ .
如图,等边△ABC 的顶点都在 ⊙O 上,点D 是 ⊙O 上一点,∠BDC = ____ .
... ... ...
圆周角PPT,第四部分内容:直径对直角
如果圆周角定理中的圆弧变成了半圆,就会有如下推论:
半圆(或直径)所对的圆周角是直角
反过来,也成立
90°的圆周角所对的弦是直径
例题
如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm,∠ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.
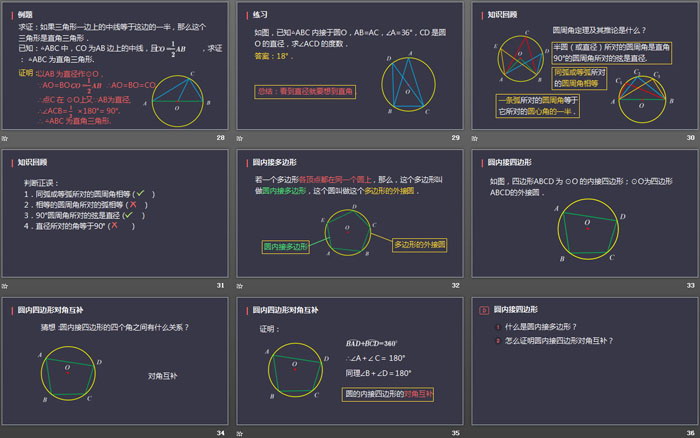
求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
... ... ...
圆周角PPT,第五部分内容:知识回顾
圆周角定理及其推论是什么?
半圆(或直径)所对的圆周角是直角 90°的圆周角所对的弦是直径.
同弧或等弧所对的圆周角相等
一条弧所对的圆周角等于它所对的圆心角的一半.
判断正误:
1.同弧或等弧所对的圆周角相等( )
2.相等的圆周角所对的弧相等( )
3.90°圆周角所对的弦是直径( )
4.直径所对的角等于90°( )
... ... ...
圆周角PPT,第六部分内容:圆内接多边形
若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
圆内接四边形
如图,四边形ABCD 为 ⊙O 的内接四边形;⊙O为四边形ABCD的外接圆.
圆内四边形对角互补
猜想:圆内接四边形的四个角之间有什么关系?
... ... ...
圆周角PPT,第七部分内容:圆的性质综合
如图,已知AE 是圆O 的直径,△ABC 内接于圆O,AD⊥BC 于 D 交圆O于F.
(1)求证:∠BAE =∠CAF.
(2) 若∠ACB =60°,CF =2,求圆O 的半径.
(1)提示:连接EC
(2)提示:连接OF,OC
... ... ...
圆周角PPT,第八部分内容:总结
这节课我们学会了什么?
半圆(或直径)所对的圆周角是直角 90°的圆周角所对的弦是直径.
同弧或等弧所对的圆周角相等
一条弧所对的圆周角等于它所对的圆心角的一半.
若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
圆的内接四边形的对角互补
关键词:人教版九年级上册数学PPT课件免费下载,圆周角PPT下载,圆PPT下载,.PPT格式;











